14 мая 2011 в 01:10

Подсчет объектов на бинарном изображении. Часть 1

Аннотация

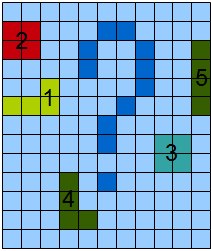
Раз, два, три, четыре, пять. Будем в прятки мы играть. В статье рассказывается про алгоритм разметки (или подсчета) объектов на бинарном изображении и о том, как без дополнительного прохода вычисляются (в еще неопубликованной части 2) геометрические характеристики этих объектов. Алгоритмы подобного типа часто используются при распознавании образов на бинарном препарате и показывают свою вычислительную эффективность.
В завершении статьи, читателям предлагается интересная задачка, грамотное решение которой существует и необходимо, при практической реализации алгоритма. Приводится исходный код, но в отличии от предыдущих моих постов, он выполнен не на языке MatLab а в абсолютно свободной, не менее мощной среде SciLab.
Source Code Highlighter.

Листинг 1 — рекурсивная реализация алгоритма разметки связных областей.

Это все нам не подходит.
Область пикселей будем называть связной, если для каждого пикселя из этой области существует сосед из этой же области. Про виды связности я приводил иллюстрацию в этом топике(Рис.1,2). Наш алгоритм будет четырех связным, хотя его без особых умственных усилий можно переделать и для восьми связного варианта.

Однопроходный, не рекурсивный алгоритм разметки

Идея данного алгоритма основана на использовании уголка — ABC-маски, которая показана на рисунке 3.

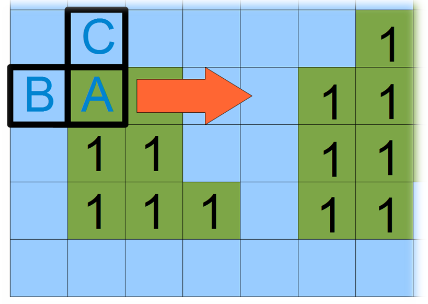Рисунок 3 — ABC маска и направление последовательного сканирования изображения.

Проход по изображению данной маской осуществляется слева-направо и сверху-вниз. Считается, что за границей изображения объектов нет, поэтому, если туда попадают B или C — это требует дополнительной проверки при сканировании. На рисунке 4 изображены 5 возможных позиций маски на изображении.
Рассмотрим их.

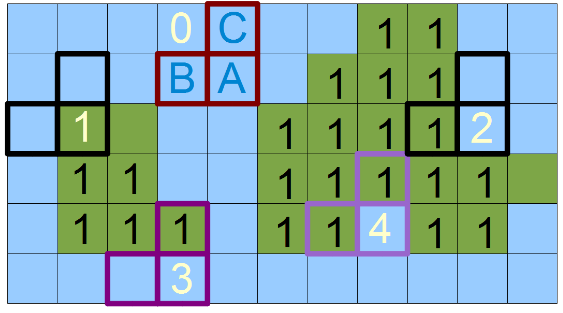Рисунок 4 — Пять возможных позиций ABC-маски

Позиция под номером 0, когда не размечены все три компонента маски — в этом случае мы просто пропускаем пиксель.
Позиция под номером 1, когда помечен только элемент A — в этом случае мы говорим о создании нового объекта — новый номер.
Позиция под номером 2, когда помечен элемент элемент B — в этом случае мы помечаем текущий пиксель A меткой, расположенной в B.
Позиция под номером 3, когда помечен элемент элемент С — в этом случае мы помечаем текущий пиксель A меткой, расположенной в С.
Позиция под номером 4, тогда мы говорим о том, что метки (номера объектов) B и C связаны — то есть эквивалентны и пиксель A может быть помечен либо как B либо как C. В некоторых реализация составляют граф эквивалентности таких меток, с последующим его разбором, однако на мой взгляд в это нет необходимости. Мы будем делать так — в том случае, если B не равно C то перенумеруем все уже обработанные пиксели помеченные как С в метку B. Но об этом в самом конце.

Ближе к реализации.
В начале создадим тестовые данные аналогичные изображенным на рисунке 2, а именно матрицу Image состоящую из нулей и единичек.
Image = [0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 1 0 0;
0 1 1 1 1 0 0 1 1 1 1;
0 1 1 1 1 0 0 0 0 0 0;
0 1 1 1 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 1 1 0 0;
0 0 0 0 0 0 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 1 1;
0 1 1 1 0 1 1 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0]
Matplot(Image*255) // Посмотрим на нашу матрицу как на картинке
[m,n]=size(Image); // Узнаем горизонтальный и вертикальные размеры матрицы
km = 0; kn = 0; // Они нам еще пригодятся
cur = 1; // Переменная для подсчета объектов

* This source code was highlighted with Source Code Highlighter.

Листинг 2 — инициализация исходных данных.

А затем пройдемся по изображению выполняя серию простых и очевидных проверок. ABC-маска, которой мы проходим по картинке, проиллюстрирована на рисунке 3. Возможные комбинации, которые проверяются этой маской изображены на рисунке 4.
// Цикл по пикселям изображения
for i = 1:1:m
for j = 1:1:n
kn = j - 1;
if kn <= 0 then
kn = 1;
B = 0;
else
B = Image(i,kn); // Смотри рисунок 3 в статье
end
km = i - 1;
if km <= 0 then
km = 1;
C = 0;
else
C = Image(km,j); // Смотри рисунок 3 в статье
end
A = Image(i,j); // Смотри рисунок 3 в статье
if A == 0 then // Если в текущем пикселе пусто - то ничего не делаем
elseif B == 0 & C == 0 then // Если вокруг нашего пикселя пусто а он не пуст - то это повод подумать о новом объекте
cur = cur + 1;
Image(i,j) = cur;
elseif B ~=0 & C == 0 then
Image(i,j) = B;
elseif B == 0 & C ~= 0 then
Image(i,j) = C;
elseif B ~= 0 & C ~= 0 then
if B == C then
Image(i,j) = B;
else
Image(i,j) = B;
Image(Image == C) = B;
end
end
end
end

* This source code was highlighted with Source Code Highlighter.

Листинг 3 — последовательное сканирование пикселей изображения и разметка связных областей.

Результатом выполнения этого скрипта будет размеченная матрица:

Рисунок 5 — Результат выполнения листингов 2 и 3 — объектам присвоены уникальные номера.

Недостаток — номера не последовательны, однако это по большому счету абсолютно не нужно, но исправляется дополнительными модификациями алгоритма.

В заключение первой части статьи — перенумерацию меток можно вообще не делать, если умным образом использовать матрицу указателей на специальную структуру. Над этим я предлагаю поразмыслить читателю. На языке SciLab не получится реализовать версию с указателями, однако в последней третьей части статьи я это сделаю с использованием псевдокода.

Что будет во второй части — в ней будет рассказано об эмпирических факторах форм объектов, компактности и факторе Малиновского. Мы посмотрим уникальную иллюстрацию, над которой я сейчас работаю, на которой плавное изменение формы объекта отражается возрастанием или падением его фактора-формы.

Спасибо всем прочитавшим, жду ваших отзывов.

Ссылки и использованные источники

[1] Алгоритмы / Подсчёт объектов на изображении ссылка (видимо эта статья когда-то была на Хабре, но найти не удалось)
[2] Лекция: Анализ информации содержащейся в изображении ссылка на ppt файл

Разметка связных областей делается с помощью bwlabel (есть и для Scilab).

Вычисление характеристик (длина, площадь) с помощью встроенных функций (если есть) или в матричном виде, аккумулируя результаты с помощью vl_binsum, histc или подобных.

Всяко будет красивее и быстрее, чем писать циклы в Matlab/Scilab.

Вот например на днях нужно было посчитать длину общей границы между всеми парами областей: (чуть более сложная задача, чем посчитать длины границ объектов):
function adj = pairwiseBoundaryLengths(map) % map содержит разметку изображения по областям h = size(map, 1); w = size(map, 2); n = max(map(:)); % вертикальные и горизонтальные границы % фокус - записываем для каждой границы номера граничащих областей % но разворачиваем пару чисел в одномерный индекс, чтобы проще было потом суммировать vertical = (map(1 : h - 1, :) - 1) * n + map(2 : h, :); horizontal = (map(:, 1 : w - 1) - 1) * n + map(:, 2 : w); adj = zeros(n); adj(:) = vl_binsum(adj(:), 1, vertical(:)); adj(:) = vl_binsum(adj(:), 1, horizontal(:)); adj = adj + adj'; adj = adj .* (ones(n) - eye(n)); end
Не понадобился ни один цикл.

А ещё, у вас операция слияния областей «Image(Image == C) = B;» может оказаться дороговатой.

Проходиться при каждом слиянии по всему изображению, заменяя метки? Не дольше ли это окажется обычного dfs/bfs, который, по крайней мере, работает за линейное время? Можно использовать для быстрого объединения непересекающиеся множества, но всё равно будет долго, неподходящий язык выбран для такой задачи.

Потому и предоставляется готовая функция bwlabel, написанная на C.

В пункте 5-ом, описания позиции маски, говорится как раз о перенумерации Image(Image == C) = B. При реальной рализации это эфективно делать с использованием указатлей — см. задачку в самом конце статьи.

У меня получилось сделать однопроходный алгоритм (C++) без использования структур/множеств. Храню массив int* вместо int, и в случае, когда текущий пиксель объединяет 2 объекта (последний else у вас в коде), делаю так:

int **m_labels; ... } else { if (*m_labels[bIndex] <= *m_labels[cIndex]) *m_labels[cIndex] = *m_labels[bIndex]; else *m_labels[bIndex] = *m_labels[cIndex]; m_labels[index] = m_labels[bIndex]; }
т.е. изменяю значение указателя с бОльим номером объекта на значение объекта с меньшим номером, с которым происходит объединение. Таким образом остается один (общий) объект с меньшим номером. int* в качестве ячейки позволяет изменить номер объекта для всех пикселей этого объекта без дополнительного прохода по массиву рисунка.

Конечно, для такой реализации необходимо иметь матрицу указателей, но в моем случае массив рисунка для этих нужд я использовать не мог.

Пока еще не понял будет ли это работать для всех коллизий, однако идея очень интересная.
Вот к примеру пусть разметка такова, что возникают последовательно эквивалентности:
2 эквивалентно 3, затем: 3 эквивалентно 5.
1. По адресу в указателе на 2 ставится 3.
2. По адресу указывающему на на 3 ставится 5.
Таким образом коллизия не разрешена и перенумерация выполнена не полностью: осталось и 3 и 5. Когда должно остаться только 5.
Или я где-то заблуждаюсь?

1. Соединяются объекты 2 и 3. Объект 3 станет объектом 2.
2. Соединяются объекты 3 и 5. Объект 5 станет объектом 2, т.к. объект 3 — уже имеет номер 2 (переименован в предыдущем шаге)

Код работает, я сейчас использую этот подход в реальном проекте (кстати, спасибо вам за отличную статью, очень своевременно для меня).

Ксати, что характерно, если не делать проверку

} else { if (*m_labels[bIndex] <= *m_labels[cIndex]) *m_labels[cIndex] = *m_labels[bIndex]; else *m_labels[bIndex] = *m_labels[cIndex]; m_labels[index] = m_labels[bIndex]; }
а делать просто

} else { *m_labels[cIndex] = *m_labels[bIndex]; m_labels[index] = m_labels[bIndex]; }
то выйдет криво (будет куча объектов вместо одного).

данную задачу можно решить существенно быстрее и сильно сэкономив память.
сначала обходим объект по внешнему контуру (можно сделать за время порядка количества внешних точек, что обычно не больше 4*X*Y, если интересно, могу написать как делается), а потом заполняем соответствующим индексом все внутренние точки (если это нужно).

остается только уметь находить начальные точки для обхода, без предварительного квадратичного (X*Y) прохода по изображению это сделать сложно, но можно совместить этот процесс с считыванием изображения.